what to include in table of multiple regression
by Sharad Vijalapuram
How to read a Regression Table
What is regression?
Regression is i of the most important and commonly used data assay processes. Only put, information technology is a statistical method that explains the forcefulness of the relationship between a dependent variable and one or more than contained variable(south).
A dependent variable could be a variable or a field you are trying to predict or sympathise. An independent variable could be the fields or data points that yous think might have an impact on the dependent variable.
In doing and then, information technology answers a couple of important questions —
- What variables matter?
- To what extent do these variables thing?
- How confident are we nearly these variables?
Let's take an example…
To better explicate the numbers in the regression table, I thought information technology would be useful to utilize a sample dataset and walk through the numbers and their importance.
I'm using a small dataset that contains GRE (a test that students accept to be considered for admittance in Grad schools in the US) scores of 500 students and their gamble of admittance into a university.
Because risk of admittance depends on GRE score, take chances of admittance is the dependent variable and GRE score is the contained variable.

Regression line
Drawing a straight line that best describes the relationship between the GRE scores of students and their chances of admittance gives u.s.a. the linear regression line. This is known every bit the trend line in various BI tools. The bones idea backside cartoon this line is to minimize the distance betwixt the data points at a given x-coordinate and the y-coordinate through which the regression line passes.
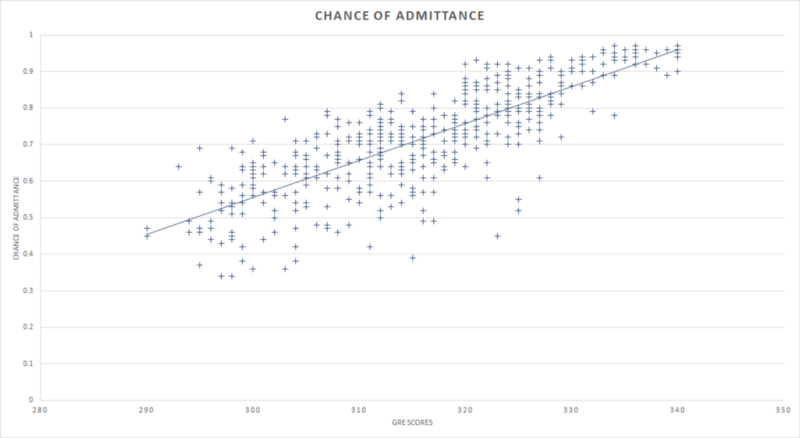
The regression line makes information technology easier for us to represent the relationship. It is based on a mathematical equation that associates the x-coefficient and y-intercept.
Y-intercept is the signal at which the line intersects the y-axis at x = 0. It is too the value the model would accept or predict when x is 0.
Coefficients provide the touch on or weight of a variable towards the entire model. In other words, it provides the amount of change in the dependent variable for a unit change in the contained variable.
Computing the regression line equation
In order to find out the model's y-intercept, we extend the regression line far enough until it intersects the y-centrality at x = 0. This is our y-intercept and information technology is effectually -ii.5. The number might not really make sense for the data set we are working on only the intention is to simply show the calculation of y-intercept.

The coefficient for this model will just be the slope of the regression line and tin be calculated by getting the change in the comprisal over the change in GRE scores.

In the example above, the coefficient would just be
g = (y2-y1) / (x2-x1)
And in this case, it would be close to 0.01.
The formula y = thou*x + b helps us calculate the mathematical equation of our regression line. Substituting the values for y-intercept and slope we got from extending the regression line, nosotros can codify the equation -
y = 0.01x — ii.48
-two.48 is a more accurate y-intercept value I got from the regression table as shown afterward in this postal service.
This equation lets u.s. forecast and predicts the take a chance of admittance of a pupil when his/her GRE score is known.
Now that nosotros have the basics, let's jump onto reading and interpreting a regression table.
Reading a regression table
The regression table can be roughly divided into 3 components —
- Analysis of Variance (ANOVA): provides the analysis of the variance in the model, every bit the proper noun suggests.
- regression statistics: provide numerical information on the variation and how well the model explains the variation for the given data/observations.
- remainder output: provides the value predicted past the model and the difference between the actual observed value of the dependent variable and its predicted value by the regression model for each data point.
Assay of Variance (ANOVA)

Degrees of liberty (df)
Regression df is the number of independent variables in our regression model. Since we only consider GRE scores in this instance, it is 1.
Residual df is the total number of observations (rows) of the dataset subtracted by the number of variables beingness estimated. In this example, both the GRE score coefficient and the constant are estimated.
Residual df = 500 — 2 = 498
Total df — is the sum of the regression and residual degrees of freedom, which equals the size of the dataset minus one.
Sum of Squares (SS)

Regression SS is the total variation in the dependent variable that is explained by the regression model. It is the sum of the square of the departure between the predicted value and mean of the value of all the data points.
∑ (ŷ — ӯ)²
From the ANOVA table, the regression SS is 6.5 and the total SS is 9.9, which means the regression model explains about vi.five/nine.ix (around 65%) of all the variability in the dataset.
Residual SS — is the total variation in the dependent variable that is left unexplained by the regression model. It is likewise chosen the Error Sum of Squares and is the sum of the foursquare of the difference between the actual and predicted values of all the data points.
∑ (y — ŷ)²
From the ANOVA tabular array, the residual SS is about 3.iv. In full general, the smaller the error, the amend the regression model explains the variation in the data set and and so we would ordinarily desire to minimize this error.
Total SS — is the sum of both, regression and rest SS or by how much the hazard of admittance would vary if the GRE scores are Non taken into account.
Mean Squared Errors (MS) — are the mean of the sum of squares or the sum of squares divided by the degrees of freedom for both, regression and residuals.
Regression MS = ∑ (ŷ — ӯ)²/Reg. df
Residual MS = ∑ (y — ŷ)²/Res. df
F — is used to test the hypothesis that the slope of the independent variable is zero. Mathematically, it can also exist calculated equally
F = Regression MS / Residual MS
This is otherwise calculated past comparing the F-statistic to an F distribution with regression df in numerator degrees and residual df in denominator degrees.
Significance F — is nix but the p-value for the null hypothesis that the coefficient of the independent variable is cipher and as with any p-value, a low p-value indicates that a significant relationship exists betwixt dependent and contained variables.

Standard Error — provides the estimated standard deviation of the distribution of coefficients. It is the amount by which the coefficient varies across different cases. A coefficient much greater than its standard error implies a probability that the coefficient is not 0.
t-Stat — is the t-statistic or t-value of the test and its value is equal to the coefficient divided by the standard error.
t-Stat = Coefficients/Standard Fault
Again, the larger the coefficient with respect to the standard mistake, the larger the t-Stat is and higher the probability that the coefficient is abroad from 0.
p-value — The t-statistic is compared with the t distribution to decide the p-value. We usually only consider the p-value of the independent variable which provides the likelihood of obtaining a sample every bit close to the one used to derive the regression equation and verify if the slope of the regression line is actually zero or the coefficient is close to the coefficient obtained.
A p-value below 0.05 indicates 95% confidence that the slope of the regression line is non nil and hence in that location is a pregnant linear human relationship between the dependent and contained variables.
A p-value greater than 0.05 indicates that the slope of the regression line may be zero and that there is not sufficient prove at the 95% confidence level that a significant linear relationship exists between the dependent and independent variables.
Since the p-value of the independent variable GRE score is very close to 0, nosotros can exist extremely confident that there is a pregnant linear relationship between GRE scores and the chance of comprisal.
Lower and Upper 95% — Since nosotros mostly apply a sample of data to approximate the regression line and its coefficients, they are more often than not an approximation of the true coefficients and in turn the true regression line. The lower and upper 95% boundaries give the 95th confidence interval of lower and upper bounds for each coefficient.
Since the 95% confidence interval for GRE scores is 0.009 and 0.01, the boundaries practice not contain nix so, we tin be 95% confident that there is a significant linear relationship betwixt GRE scores and the chance of comprisal.
Delight note that a confidence level of 95% is widely used but, a level other than 95% is possible and can be set during regression analysis.
Regression Statistics

R² (R Square) — represents the power of a model. Information technology shows the amount of variation in the dependent variable the independent variable explains and always lies between values 0 and 1. As the R² increases, more than variation in the data is explained by the model and meliorate the model gets at prediction. A low R² would indicate that the model doesn't fit the data well and that an contained variable doesn't explain the variation in the dependent variable well.
R² = Regression Sum of Squares/Total Sum of Squares
Withal, R square cannot determine whether the coefficient estimates and predictions are biased, which is why you must assess the residual plots, which are discussed later in this commodity.
R-foursquare too does not indicate whether a regression model is acceptable. Y'all can have a low R-squared value for a good model, or loftier R-squared value for a model that does not fit the data.
R², in this case, is 65 %, which implies that the GRE scores tin can explain 65% of the variation in the chance of admittance.
Adapted R² — is R² multiplied past an adjustment factor. This is used while comparing dissimilar regression models with different independent variables. This number comes in handy while deciding on the correct contained variables in multiple regression models.
Multiple R — is the positive square root of R²
Standard Error — is unlike from the standard fault of the coefficients. This is the estimated standard deviation of the fault of the regression equation and is a adept measure of the accurateness of the regression line. It is the foursquare root of the residual mean squared errors.
Std. Error = √(Res.MS)
Residual Output
Residuals are the difference betwixt the actual value and the predicted value of the regression model and residual output is the predicted value of the dependent variable past the regression model and the residual for each information signal.
And as the proper name suggests, a residual plot is a scatter plot between the balance and the independent variable, which in this case is the GRE score of each student.
A residual plot is important in detecting things like heteroscedasticity, non-linearity, and outliers. The process of detecting them is not beingness discussed as part of this article but, the fact that the residual plot for our case has information scattered randomly helps united states in establishing the fact that the relationship between the variables in this model is linear.

Intent
The intent of this commodity is not to build a working regression model just to provide a walkthrough of all the regression variables and their importance when necessary with a sample data prepare in a regression table.
Although this article provides an caption with a unmarried variable linear regression every bit an example, delight be aware that some of these variables could have more importance in the cases of multi-variable or other situations.
References
- Graduate Admissions Dataset
- ten things about reading a regression table
- A refresher on regression analysis
Larn to code for gratis. freeCodeCamp's open source curriculum has helped more xl,000 people get jobs as developers. Go started
Source: https://www.freecodecamp.org/news/https-medium-com-sharadvm-how-to-read-a-regression-table-661d391e9bd7-708e75efc560/
0 Response to "what to include in table of multiple regression"
Post a Comment